Solution for Linear Equation Using Elementary Row Operation

I know the first three represent a square matrix, but are the vectors column vectors or row vectors? A matrix is made up of column vectors. Is the top row of the square. So the top row is. You will end up with the identity matrix on the left of your augmented matrix, with: There was something that I missed - sometimes you just need to see someone else lay it out before you can fit the rest of the puzzle. Thank you very much. We all have those moments, no problem, happy to help! Nice feedback here, as well!

Matrix row operations

Sign up or log in Sign up using Google. Sign up using Facebook. Sign up using Email and Password. Okay, so how do we use augmented matrices and row operations to solve systems? Once we have the augmented matrix in this form we are done. To convert it into the final form we will start in the upper left corner and work in a counter-clockwise direction until the first two columns appear as they should be.

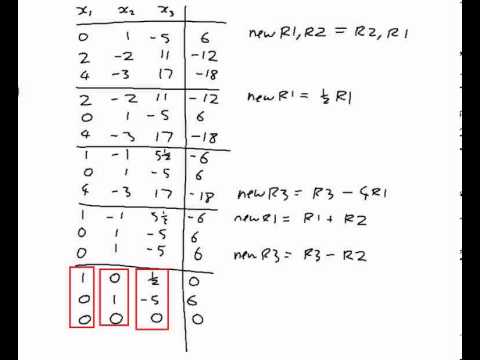
So, the first step is to make the red three in the augmented matrix above into a 1. We should always try to minimize the work as much as possible however. The next step is to get a zero below the 1 that we just got in the upper left hand corner.

Using Elementary Row Operations to Solve for Systems of Equations Tutorial | Sophia Learning

This means that we need to change the red three into a zero. This will almost always require us to use third row operation. If we add -3 times row 1 onto row 2 we can convert that 3 into a 0.

Here is that operation. Next, we need to get a 1 into the lower right corner of the first two columns. This means changing the red into a 1. This is usually accomplished with the second row operation. If we divide the second row by we will get the 1 in that spot that we need. The final step is to turn the red three into a zero. Again, this almost always requires the third row operation. Here is the operation for this final step. We will mark the next number that we need to change in red as we did in the previous part.

• Solving Systems of Linear Equations; Row Reduction - HMC Calculus Tutorial.
• Elementary matrix row operations.
• Successful Christian Living.
• Using Elementary Row Operations to Determine A−1.

However, the only way to change the -2 into a zero that we had to have as well was to also change the 1 in the lower right corner as well. Sometimes it will happen and trying to keep both ones will only cause problems.

• Gods Potpourri of Love.
• Die Rezeption von fiktionaler Gewalt im Fernsehen und deren mögliche Auswirkung (German Edition).
• Wer auf die Liebe wartet ... (Bianca 1871) (German Edition)?
• .

It is important to note that the path we took to get the augmented matrices in this example into the final form is not the only path that we could have used. There are many different paths that we could have gone down. All the paths would have arrived at the same final augmented matrix however so we should always choose the path that we feel is the easiest path. Note as well that different people may well feel that different paths are easier and so may well solve the systems differently. They will get the same solution however.

• Sternzeichengedichte - Steinbock (German Edition)?
• Matrix row operations (article) | Matrices | Khan Academy.
• Using Elementary Row Operations to Determine A−1.
• Matrix row operations!
• Da Nang Postscripts?
• Atomic Kingdom: If Iran Builds the Bomb, Will Saudi Arabia Be Next?;

For two equations and two unknowns this process is probably a little more complicated than just the straight forward solution process we used in the first section of this chapter. This process does start becoming useful when we start looking at larger systems. As with two equations we will first set up the augmented matrix and then use row operations to put it into the form,. As with the previous examples we will mark the number s that we want to change in a given step in red. The first step here is to get a 1 in the upper left hand corner and again, we have many ways to do this.

Note as well that this will almost always require the third row operation to do. Also, we can do both of these in one step as follows. So, we got a fraction showing up here. The next step is to change the 3 below this new 1 into a 0.

Using Elementary Row Operations to Solve for Systems of Equations

Sometimes it is just as easy to turn this into a 0 in the same step. Next, we need to get the number in the bottom right corner into a 1. We can do that with the second row operation. Now, we need zeroes above this new 1. So, using the third row operation twice as follows will do what we need done. That was only because the final entry in that column was zero. The final step is then to make the -2 above the 1 in the second column into a zero.