Integrated Cost-Schedule Risk Analysis

Let be the frequency of the cost interval and let be that of the duration interval. Thus, the marginal probability density functions of cost and schedule are defined as As a result, the marginal cumulative probability distribution functions are Accordingly, the independent risk probability distribution functions are.

The integrated cost and schedule risk is defined as the probability of failing to complete the project under a specified objective with respect to cost and schedule. The integrated cost and schedule frequency statistics is shown in Figure 1. Let be the frequency of the shadow region in Figure 1.

Then the integrated cost and schedule probability density function is.

Integrated Cost and Schedule Risk Analysis

The integrated probability distribution function in region is where is the cumulative frequency of simulation outputs which fall on the shadow region. Accordingly, the integrated cost and schedule risk probability distribution function is. The conditional probability density functions of cost and schedule are The conditional probability distribution functions of cost and schedule are. The OCAV is composed of six subsystems. To focus on the simulation-based method presented in this paper, we name the six subsystems as subsystems 1 to 6 instead of their actual names.

In this model, we assume that the parameters of duration and cost are random variables and both of them follow the triangular distribution: The parameters are estimated by project managers in a subjective manner or assessed through historical data.

Account Options

From the simulation output, we can get pairs of data of total cost and duration ,. Using frequency statistical method, the simulation outputs are grouped as and , respectively.

According to statistics, we obtain the marginal frequency distribution of total cost , the marginal frequency distribution of total duration , and the integrated bivariate frequency distribution , and the results are shown in Table 2. We can also obtain the following results. More specifically, the theoretical probability distribution functions of the total cost and duration are subject to and , respectively.

Besides, the distribution curves are shown in Figures 3 and 4.

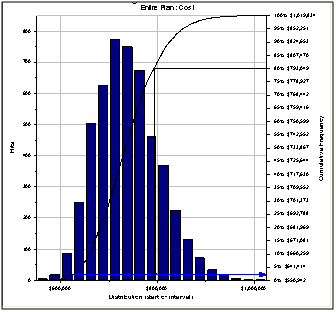
Hence, interval estimation of parameter can be carried out. We can get the marginal probability density functions of the total cost and total duration and , the marginal probability distribution functions and , and the marginal risk probability distribution functions and by substituting data into formulas 1 — 3 ; all the results are shown in Table 3.

Productspecificaties

The marginal probability distribution and the marginal risk probability distribution of the total cost and the total duration are shown in Figures 5 and 6 , respectively. According to formulas 6 and 7 , we can get the integrated probability distribution of the total cost and duration in Table 4 and the integrated risk probability distribution of total cost and duration in Table 5. According to the data in Table 5 , we draw the curved surface of integrated risk probability distribution of total cost and duration in Figure 7. According to formula 9 , we can get the conditional probability density distributions of the total cost and total duration and in Tables 6 and 7.

• 1st Edition.
• Samenvatting.
• Samenvatting!
• The Project Schedule is the Platform for Both Schedule Risk and Cost Risk Analysis?
• Les Employés d’abord, les clients ensuite : Comment renverser les règles du management (French Edition).
• JMP 11 Fitting Linear Models!
• www.newyorkethnicfood.com | Integrated Cost-Schedule Risk Analysis (ebook), Hulett, David | | Boeken.

According to the above results, the smooth curves of conditional probability distribution of the total cost and the total duration are drawn in Figures 8 and 9. Using goodness of fit test method, we infer that the conditional probability distributions of the total cost and the total duration follow normal distributions, and the goodness of fit is good.

Meanwhile, the mean and the standard deviation of the conditional probability distribution are obtained. The results are shown in Table 8 ; the computational process is similar to the following example: Through the data in Table 5 , we establish the integrated risk space surface of two-dimensional continuous random vector of the cost and duration.

• The Stewardess.
• Vegetarian Cooking: Vege Pork, Winter Melon and King Trumpet Mushroom Soup (Vegetarian Cooking - Soups with Vege Meats Book 18).
• Faefever (Mackayla Lane Book 3)!
• The Emergence of the Race Issue in W.E.B. Du Bois Life!
• Productspecificaties;
• Asymptotic Geometric Analysis: Proceedings of the Fall 2010 Fields Institute Thematic Program: 68 (Fields Institute Communications).

Also, we obtain the integrated risk probability approximation under cost and duration constraints by surface interpolation method. For example, is the risk probability value under constraints of the total cost thousand RMB and the total duration months. In Figure 6 , when the number of simulations is large enough, the small curved surface which consisted of , , , and can be considered as a plane.

Integrated Cost-Schedule Risk Analysis

In order to avoid underestimating the probability value, we choose , , and which have higher risk probability to establish equation: After that, the risk probability value is acquired under constraints of total cost and total duration. We can substitute , , into 14 to gain. Following the definition of the conditional probability distribution function and the marginal probability distribution function, the integrated risk probability of the total cost and duration is calculated as follows: For example, we also get the risk probability value under the integrated constraints of the total cost ten thousand RMB and the total duration months.

There are effective ways to estimate the impact on the cost of complex projects from project risks of all types, including traditional cost-type risks and the indirect but often substantial impact from risks usually thought of as affecting project schedules. Integrated cost-schedule risk anlaysis helps us determine how likely the project will go over budget with the current plan, how much contingency reserve is required to achieve a desired level of certainty, and which risks are most important so the project manager can mitigate them and achieve a better result.

Integrated Cost-Schedule Risk Analysis provides solutions for these and other challenges. It focuses on the way that schedule risk can generate cost risk, and how to handle this relationship. It also applies the Risk Driver Method to the analysis so that you can clearly and transparently identify the key risks, rather than just the most risky cost line items.

Analyzing Integrated Cost-Schedule Risk for Complex Product Systems R&D Projects

With detailed worked examples and over 70 illustrations, Integrated Cost-Schedule Risk Analysis offers the definitive guide to this critically important aspect of project management from surely the world's leading commentator. Toon meer Toon minder. Overige kenmerken Extra groot lettertype Nee. One study of public transportation infrastructure projects found that 9 out of 10 projects had overrun their initial estimates and that overruns of 50 to percent were common.

We make the following observations regarding the distribution of inaccuracies of construction cost estimates. Costs are underestimated in almost 9 out of 10 projects. For a randomly selected project, the likelihood of actual costs being larger than estimated costs is 86 percent. The likelihood of actual costs being lower than or equal to estimated costs is 14 percent. Flyvbjerg also cites that cost estimating accuracy overruns averaged