Aperiodic Crystals

In order that the quasicrystal itself be aperiodic, this slice must avoid any lattice plane of the higher-dimensional lattice. De Bruijn showed that Penrose tilings can be viewed as two-dimensional slices of five-dimensional hypercubic structures. The mathematical counterpart of physical diffraction is the Fourier transform and the qualitative description of a diffraction picture as 'clear cut' or 'sharp' means that singularities are present in the Fourier spectrum. There are different methods to construct model quasicrystals.

These are the same methods that produce aperiodic tilings with the additional constraint for the diffractive property. Thus, for a substitution tiling the eigenvalues of the substitution matrix should be Pisot numbers. The aperiodic structures obtained by the cut-and-project method are made diffractive by choosing a suitable orientation for the construction; this is a geometric approach that has also a great appeal for physicists.

Classical theory of crystals reduces crystals to point lattices where each point is the center of mass of one of the identical units of the crystal. The structure of crystals can be analyzed by defining an associated group. Quasicrystals, on the other hand, are composed of more than one type of unit, so, instead of lattices, quasilattices must be used.

Instead of groups, groupoids , the mathematical generalization of groups in category theory , is the appropriate tool for studying quasicrystals. Using mathematics for construction and analysis of quasicrystal structures is a difficult task for most experimentalists. Computer modeling, based on the existing theories of quasicrystals, however, greatly facilitated this task. Advanced programs have been developed [33] allowing one to construct, visualize and analyze quasicrystal structures and their diffraction patterns.

Navigation menu

Interacting spins were also analyzed in quasicrystals: AKLT Model and 8-vertex model were solved in quasicrystals analytically. Study of quasicrystals may shed light on the most basic notions related to quantum critical point observed in heavy fermion metals. Experimental measurements on the gold-aluminium-ytterbium quasicrystal have revealed a quantum critical point defining the divergence of the magnetic susceptibility as temperature tends to zero. Since the original discovery by Dan Shechtman , hundreds of quasicrystals have been reported and confirmed.

Undoubtedly, the quasicrystals are no longer a unique form of solid; they exist universally in many metallic alloys and some polymers. Two types of quasicrystals are known. They are periodic along this axis and quasiperiodic in planes normal to it. The second type, icosahedral quasicrystals, are aperiodic in all directions. Quasicrystals fall into three groups of different thermal stability: Except for the Al—Li—Cu system, all the stable quasicrystals are almost free of defects and disorder, as evidenced by X-ray and electron diffraction revealing peak widths as sharp as those of perfect crystals such as Si.

Diffraction patterns exhibit fivefold, threefold, and twofold symmetries, and reflections are arranged quasiperiodically in three dimensions. The origin of the stabilization mechanism is different for the stable and metastable quasicrystals. Nevertheless, there is a common feature observed in most quasicrystal-forming liquid alloys or their undercooled liquids: The icosahedral order is in equilibrium in the liquid state for the stable quasicrystals, whereas the icosahedral order prevails in the undercooled liquid state for the metastable quasicrystals.

A nanoscale icosahedral phase was formed in Zr-, Cu- and Hf-based bulk metallic glasses alloyed with noble metals. Most quasicrystals have ceramic-like properties including high thermal and electrical resistance, hardness and brittleness, resistance to corrosion, and non-stick properties. Metallic quasicrystalline coatings can be applied by plasma-coating or magnetron sputtering. A problem that must be resolved is the tendency for cracking due to the materials' extreme brittleness.

An application was the use of low-friction Al-Cu-Fe-Cr quasicrystals [41] as a coating for frying pans. However, cooking with a lot of salt would etch the quasicrystalline coating used, and the pans were eventually withdrawn from production. Shechtman had one of these pans.

Personal tools

The Nobel citation said that quasicrystals, while brittle, could reinforce steel "like armor". When Shechtman was asked about potential applications of quasicrystals he said that a precipitation-hardened stainless steel is produced that is strengthened by small quasicrystalline particles. It does not corrode and is extremely strong, suitable for razor blades and surgery instruments.

The small quasicrystalline particles impede the motion of dislocation in the material. Quasicrystals were also being used to develop heat insulation, LEDs , diesel engines, and new materials that convert heat to electricity. Shechtman suggested new applications taking advantage of the low coefficient of friction and the hardness of some quasicrystalline materials, for example embedding particles in plastic to make strong, hard-wearing, low-friction plastic gears.

The low heat conductivity of some quasicrystals makes them good for heat insulating coatings. Other potential applications include selective solar absorbers for power conversion, broad-wavelength reflectors, and bone repair and prostheses applications where biocompatibility, low friction and corrosion resistance are required. Magnetron sputtering can be readily applied to other stable quasicrystalline alloys such as Al-Pd-Mn.

While saying that the discovery of icosahedrite, the first quasicrystal found in nature, was important, Shechtman saw no practical applications. From Wikipedia, the free encyclopedia. Not to be confused with Quasi-crystals supramolecular. In his popular book What is life? Journal of Colloid Science. Dependence of island density on temperature and flux".

Pentagonal, octagonal, decagonal and dodecagonal quasicrystals". Eiler; Yunbin Guan; Lincoln S. Steinhardt; Nan Yao Proceedings of the National Academy of Sciences. A New Class of Ordered Structures". Groupoids, inverse semigroups, and their operator algebras.

Science and Technology of Advanced Materials.

Completely integrable models in quasicrystals. Volume , Number 1 , — Reports on Progress in Physics. Annual Review of Materials Research.

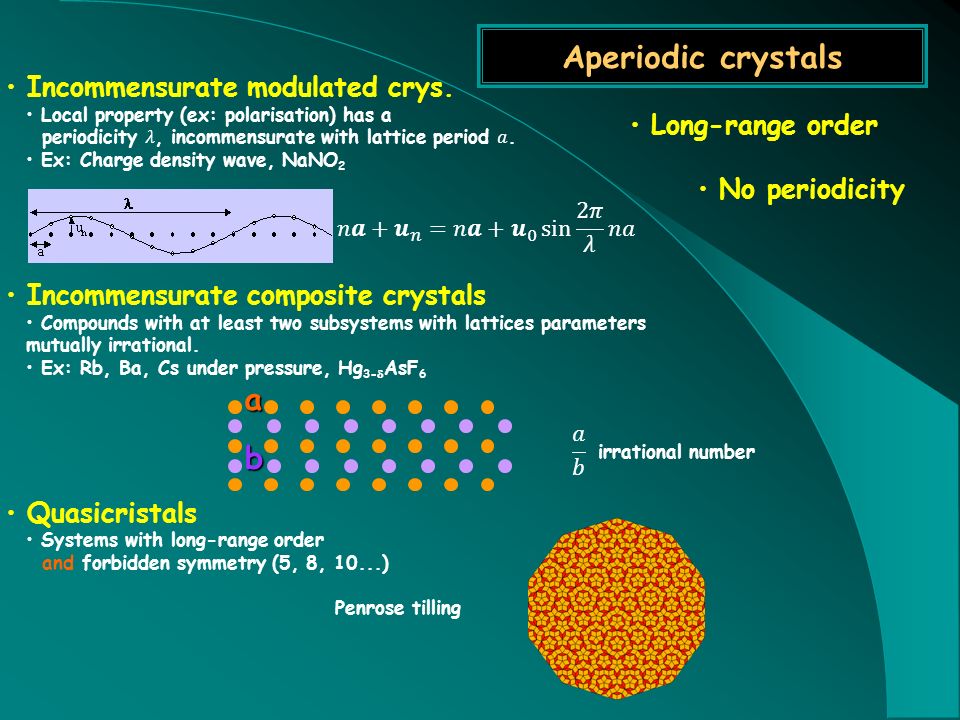
Al-Cu-Fe quasicrystalline coatings and composites studied by mechanical spectroscopy. Retrieved 12 February Statistical Self-Similarity and Fractional Dimension. Don't have an account? This chapter gives an introduction to the distinctive structural features of aperiodic crystals, including incommensurately modulated crystals, composite crystals, and quasicrystals. Atomic structures are discussed in relation to the structures of periodic crystals, while it is shown that translational symmetry is lost. Diffraction by incommensurately modulated structures is shown to give rise to Bragg reflections that can be indexed by four or more integers.

The modulation wave vector is introduced as the vector defining the periodicity of the modulation functions, as well as being the reciprocal vector employed in the indexing of Bragg reflections. Bragg reflection , composite crystal , diffraction , incommensurately modulated crystal , modulation , modulation wave vector , modulation function , quasicrystal.

Oxford Scholarship Online requires a subscription or purchase to access the full text of books within the service. Public users can however freely search the site and view the abstracts and keywords for each book and chapter. Please, subscribe or login to access full text content. To troubleshoot, please check our FAQs , and if you can't find the answer there, please contact us.

Under the terms of the licence agreement, an individual user may print out a PDF of a single chapter of a monograph in OSO for personal use for details see www. University Press Scholarship Online.