Find the Value of Z-score- Standard Normal Distribution

However, when using a standard normal distribution, we will use "Z" to refer to a variable in the context of a standard normal distribution.

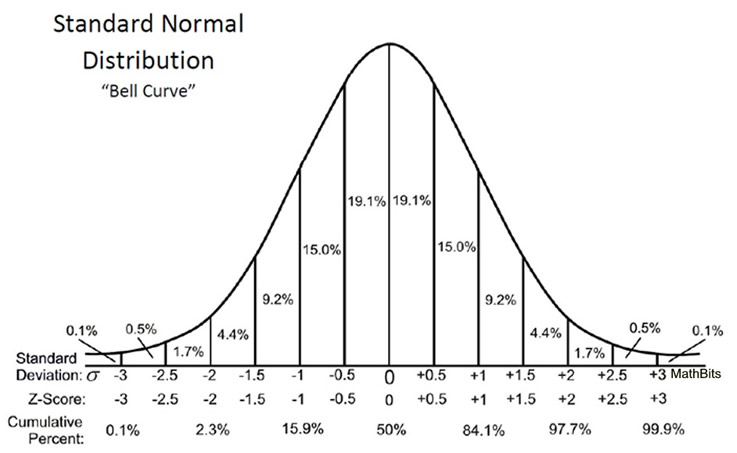
For any given Z-score we can compute the area under the curve to the left of that Z-score. The table in the frame below shows the probabilities for the standard normal distribution. Examine the table and note that a "Z" score of 0. This table is organized to provide the area under the curve to the left of or less of a specified value or "Z value". In this case, because the mean is zero and the standard deviation is 1, the Z value is the number of standard deviation units away from the mean, and the area is the probability of observing a value less than that particular Z value.

Note also that the table shows probabilities to two decimal places of Z. The units place and the first decimal place are shown in the left hand column, and the second decimal place is displayed across the top row. But let's get back to the question about the probability that the BMI is less than 30, i. We can answer this question using the standard normal distribution. The figures below show the distributions of BMI for men aged 60 and the standard normal distribution side-by-side.

The area under each curve is one but the scaling of the X axis is different. The area should be between 0 and 1.

In real life, we usually deal with normal distributions that are not standardized, so they are not expressed in z scores. Excel has several functions that will let you compute areas under the curve directly from your scores without standardizing them first.

D to different cell in Excel. You can also enter the word TRUE into a cell so you can use it in the function. Try other values of x, m and s. Returns the inverse of the normal cumulative distribution for the specified mean and standard deviation. This means that Try other values of p, m and S. D in order to get a better feeling for the use of this function. Questions about the normal distribution often ask you to calculate the area under the curve between two scores or the probability that a score would turn out to be between two scores.

The following exercise shows you how to calculate those values easily. Enter the values ,2,96, below m, S. Video transcript Here's the second problem from CK It's an open source textbook, essentially.

• By Z-Table.com?
• UsableStats: Above, Below and Between Probabilities.
• Mishaps.
• The Christian School Manifesto.
• Slither?
• Heretical Fictions: Religion in the Literature of Mark Twain.

I'm using it essentially to get some practice on some statistics problems. So here, number 2. The grades on a statistics midterm for a high school are normally distributed with a mean of 81 and a standard deviation of 6. Calculate the z-scores for each of the following exam grades. Draw and label a sketch for each example. We can probably do it all on the same example. But the first thing we'd have to do is just remember what is a z-score.

What is a z-score? A z-score is literally just measuring how many standard deviations away from the mean?

• Standard Score.
• Home Buyers Handbook.
• Probabilities of the Standard Normal Distribution Z!
• Navigation menu.
• IL GIORNO DELLORACOLO (Italian Edition)?
• Setting the scene: Part 1.
• The Naval War of 1812 Or the History of the United States Navy during the Last War with Great Britain to Which Is Appended an Account of the Battle of New Orleans.

So we literally just have to calculate how many standard deviations each of these guys are from the mean, and that's their z-scores. So let me do part a. So we have So first we can just figure out how far is 65 from the mean. Let me just draw one chart here that we can use the entire time. So it's just our distribution. We have a mean of And then a standard deviation of 6.

Your Answer

So our distribution, they're telling us that it's normally distributed. So I can draw a nice bell curve here. They're saying it's normally distributed, so that's as good of a bell curve as I'm capable of drawing. This is the mean right there at And the standard deviation is 6. So one standard deviation above and below is going to be 6.

If we go 6. Right, if we add 6, it'll get us to So that's one standard deviation below and above the mean, and then you'd add another 6. So that's a drawing of the distribution itself. So let's figure out the z-scores for each of these grades. So we first want to say, well how far is it just from our mean?

So the distance is, you just want to positive number here. Well actually, you want a negative number. Because you want your z-score to be positive or negative.