The Uncertainty Principle

It seems intuitive that if a particle exists in space, then we can point to where it is; however, the Heisenberg Uncertainty Principle clearly shows otherwise.

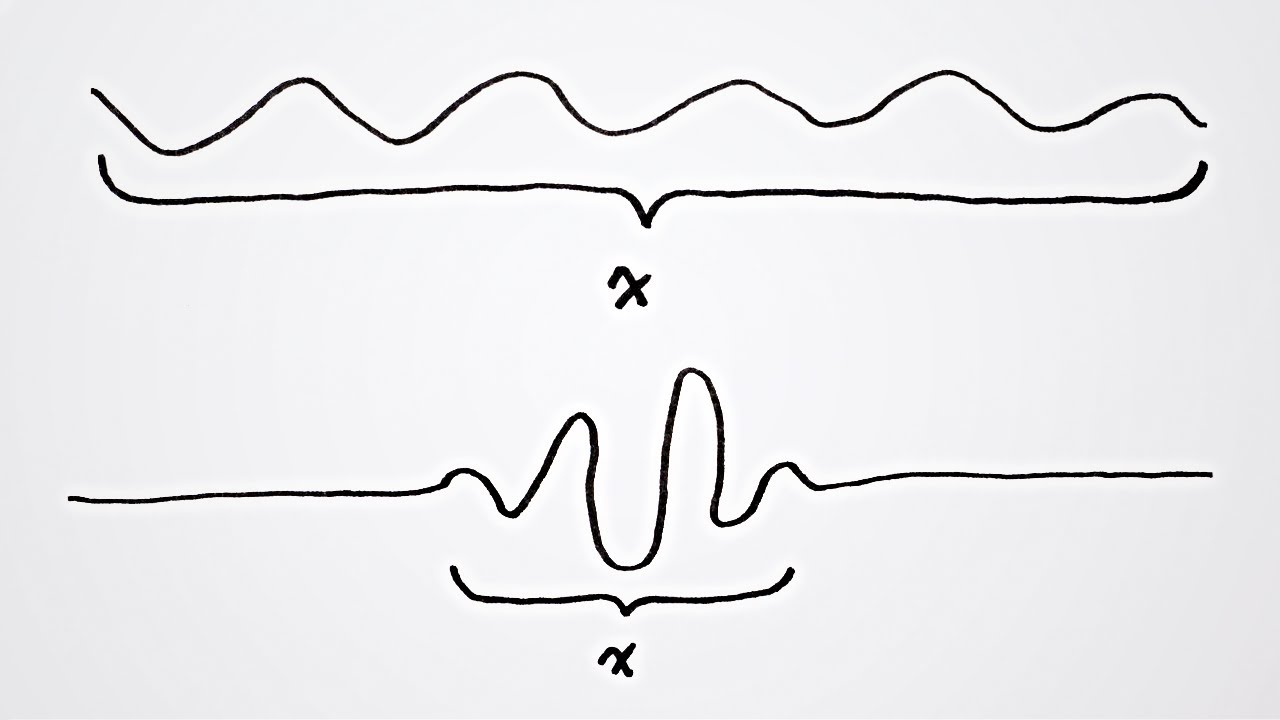
This is because of the wave-like nature of a particle. Similarly, the momentum cannot be precisely known since a particle consists of a packet of waves, each of which have their own momentum so that at best it can be said that a particle has a range of momentum. A wave packet in space. Let's consider if quantum variables could be measured exactly.

A wave that has a perfectly measurable position is collapsed onto a single point with an indefinite wavelength and therefore indefinite momentum according to de Broglie's equation. Similarly, a wave with a perfectly measurable momentum has a wavelength that oscillates over all space infinitely and therefore has an indefinite position. You could do the same thought experiment with energy and time. To precisely measure a wave's energy would take an infinite amount of time while measuring a wave's exact instance in space would require to be collapsed onto a single moment which would have indefinite energy.

The Heisenberg Principle has large bearing on practiced science and how experiments are designed. To create a measurement, an interaction with the particle must occur that will alter it's other variables. For example, in order to measure the position of an electron there must be a collision between the electron and another particle such as a photon.

This will impart some of the second particle's momentum onto the electron being measured and thereby altering it. A more accurate measurement of the electron's position would require a particle with a smaller wavelength, and therefore be more energetic, but then this would alter the momentum even more during collision. An experiment designed to determine momentum would have a similar effect on position. Consequently, experiments can only gather information about a single variable at a time with any amount of accuracy.

The volume is not the property that matters, but the mass. So if we wanted to know the diameter of that circle, we could just multiply the radius by two. So two times that number would be equal to 1.

Keep Exploring Britannica

And this is just a rough estimate of the size of the hydrogen atom using the Bohr model, with an electron in the ground state. Alright, we also did some calculations to figure out the velocity. So the velocity of an electron in the ground state of a hydrogen atom using the Bohr model, we calculated that to be 2. And since we know the mass of an electron, we can actually calculate the linear momentum.

• Heisenberg's uncertainty principle?
• What is Heisenberg's Uncertainty Principle?!
• ¡Adolescente en casa! (Spanish Edition).
• Harnessing Complexity: Organizational Implications of a Scientific Frontier.

So the linear momentum P is equal to the mass times the velocity. So we have point one here. If I want to know the uncertainty of the momentum of that electron, so the uncertainty in the momentum of that particle, momentum is equal to mass times velocity. So let's go ahead and do that.

So we would have the mass of the electron is 9. The velocity of the electron is 2. We're gonna multiply all those things together.

So we take the mass of an electron, 9. So the uncertainty in the momentum is 2. And the units would be, this is the mass in kilograms, and the velocity was in meters over seconds, so kilograms times meters per second. Alright, so this is the uncertainty associated with the momentum of our electrons. Let's plug it in to our uncertainty principle here: So we can take that uncertainty in the momentum and we can plug it in here. So now we have the uncertainty in the position of the electron in the ground state of the hydrogen atom times 2. This product must be greater than or equal to, Planck's Constant is 6.

Alright, divide that by four pi. So we could solve for the uncertainty in the position. So, Delta X must be greater than or equal to, let's go ahead and do that math.

So we have Planck's Constant, 6. So we also need to divide by the uncertainty in momentum, that's 2. So the uncertainty in the position must be greater than or equal to 2. Let's go back up here to the picture of the hydrogen atom. We welcome suggested improvements to any of our articles. You can make it easier for us to review and, hopefully, publish your contribution by keeping a few points in mind. Your contribution may be further edited by our staff, and its publication is subject to our final approval.

Unfortunately, our editorial approach may not be able to accommodate all contributions. Our editors will review what you've submitted, and if it meets our criteria, we'll add it to the article. Please note that our editors may make some formatting changes or correct spelling or grammatical errors, and may also contact you if any clarifications are needed. The Editors of Encyclopaedia Britannica. Heisenberg uncertainty principle, indeterminacy principle. Learn More in these related Britannica articles: The observables discussed so far have had discrete sets of experimental values.

Thus, one may speak of a certain average number of quanta and the actual number in any….

If an electron is bound close to the nucleus, the…. This rule, described in by the German scientist Werner Heisenberg, states that it is impossible, even in principle, to know all the details about a particular quantum system. For example, if the exact position of an electron is identified, it is….

Uncertainty principle In quantum mechanics: Heisenberg uncertainty principle quantum theory In physical science: Quantum mechanics In quantum mechanics: Hidden variables In physics: Quantum mechanics In subatomic particle: