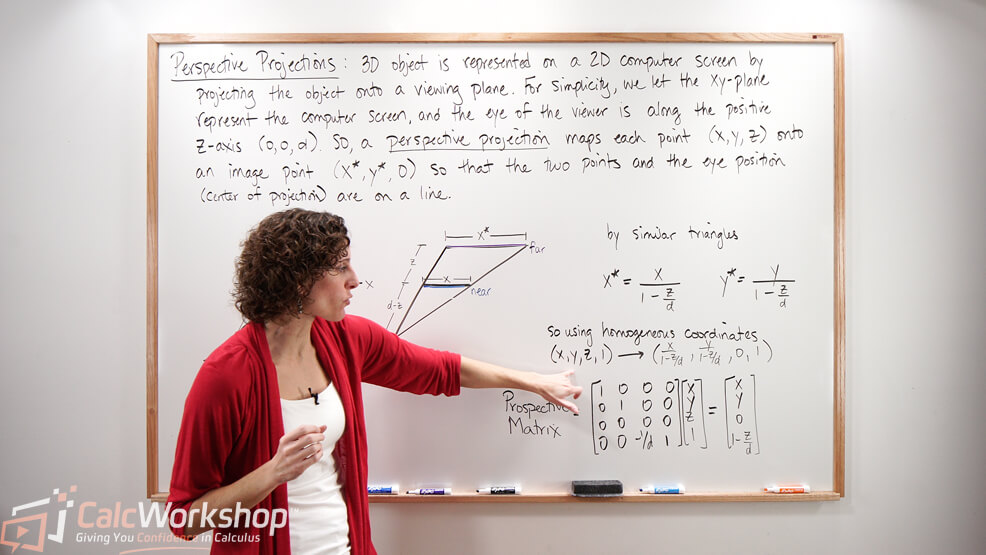Calculus for Computer Graphics

Groups - Modular Mathematics Series. A Rigorous First Course. Modern Calculus and Analytic Geometry. A Tale of Two Fractals. Building 3D Models with modo Digital Video and HD. Perspectives in Shape Analysis. Multiscale Transforms with Application to Image Processing. Latent Variable Analysis and Signal Separation. Pattern Recognition and Image Analysis. Advanced Computer-Aided Fixture Design. Complementarity and Variational Inequalities in Electronics. Game Programming using Qt 5 Beginner's Guide.

Foundation Mathematics for Computer Science. Mathematics for Computer Graphics. Rotation Transforms for Computer Graphics. Essential Computer Animation fast. Matrix Transforms for Computer Games and Animation.

Intelligent Agents for Mobile and Virtual Media. Expanding the Frontiers of Visual Analytics and Visualization. Quaternions for Computer Graphics. Imaginary Mathematics for Computer Science. How to write a great review. The review must be at least 50 characters long. The title should be at least 4 characters long. Your display name should be at least 2 characters long.

At Kobo, we try to ensure that published reviews do not contain rude or profane language, spoilers, or any of our reviewer's personal information. You submitted the following rating and review. We'll publish them on our site once we've reviewed them. Item s unavailable for purchase. Please review your cart. You can remove the unavailable item s now or we'll automatically remove it at Checkout.

I want to go through differential equations but I'm nervous about that. I'm only going into my third year of studies and I haven't really needed to do any heavy math except for some algebra and stats. I strongly recommend that you ditch the notion that everything you learn in university must necessarily be used for something specific in the future. They're trying to prepare you for the field of computer science 1 for the rest of your life, and it's not easy to predict what that might look like in 30 years. Try to become a generalist instead of a specialist.

Calculus is arguably the most significant theoretical development ever made in science, let alone mathematics. I don't think it's far fetched to require that computer scientists who work in a field brimming with mathematics have an idea of how it works. If you go into scientific computing and I know several people who came from a CS background in this field you will regret not having learned calculus. If you want to do computer graphics I can't imagine that being possible without it. Those are not the same thing. Computer science is an academical pursuit with a ton of mathematics, while programming can perhaps better be described as applied computer science.

But you don't go to university to learn how to use things, you go there to learn how things work. More important in fact, absolutely critical from a graphical point of view is linear algebra, so I'll include it since you also asked about math in gneral. This is a extremely important point. They don't know what job you're going to get.

If they did, they could just teach you exactly that. Because they don't know what job you're going to get, they have to teach you something about a lot of different jobs. Also, just because you got a job doesn't mean that you have established your career. You might have a chance to get promoted or move laterally, which could use some of your other teachings.

OJT fills in the blanks for the job you take. I spend lots of time training employees. Take everything you can while you can. There are jobs that can use all of it. Calculus is where arithmetic meets actual mathmatics. Likewise being able to handle series properly prepares you for a lot of datastructure and algorithm work.

In calculus, you are generally deriving a result by iteratively calculating a series of approximate results, and in computer science you are iteratively calculating new type s, each which is a closer approximation to your solution. So a divergent function is analogous to a non-terminating calculation.

There is a whole field of mathematics called Domain Theory which deals with these kinds of relationships.

Here, the line of thought is that a computer programs is a composition of a series of type transformers, which operate roughly analogously to the chain rule in calculus. This kind of thinking could prove particularly useful in solving problems associated with parallel computing, for instance. By helping to design languages that are built to manipulate data according to domain-theoretic constraints.

The algorithm is considered to be one of the most influential in history , as it allows us to do everything from perform signal processing for data transmission to compressing images to calculating the light spectrum of stars. I personally use FFTs on a daily basis in my job, its the core function in almost all of our data processing. Part of the reason calc is the defacto college math course is that it requires a really solid understanding of algebra, geometry and trig to do well.

Welcome to Reddit,

It's seen as a way to level the incoming population of freshmen. Many intro level courses function this way -- calc is what you should have learned in high school, into bio is what you should have learned in high school, etc. The second semester of calc is a rigorous and quantifiable introduction to inductive thinking on top of being a math course.

As others have pointed out, it has its use, but perhaps it should be made clearer that the programming is usually an implementation after the mathematical analysis has been made. So, strictly speaking, it wouldn't be necessary for programming if all you're interested in is implementing other people's algorithms and specs. If you want to go further, then some tasks require a thorough understanding of mathematics.

I've mainly used discrete algebra, probability theory and statistics for my work. Calculus itself almost never played a role, except for some details in probability theory, and when I did a hobby project on analog filters. Graph theory, OTOH, has always been really useful. While there are problems that are solved with calculus, generally calculus deals with continuous data, while computers deal with the discrete data.

There's more to computing than what computers does, and programmers will deal with continuous data as part of problem sets, mostly problems relating to how programs behave, rather than the programs themselves. Of course if you're implementing calculus problems in a program, you will use calculus.

Video games and simulations tend to do this. Use of this site constitutes acceptance of our User Agreement and Privacy Policy. Log in or sign up in seconds.

Ask a science question. Outstanding posts recognized by the mod team Weekly Features: Are you a science expert? Sign up to be a panelist!

• Landluft für Anfänger - 05: Über Mütter und Babys (German Edition).
• The Kings Commander (Jack Stewart Trilogy Book 1).
• When the Voiceless Sing: Love stories from our hero Caregivers.
• TRIPPING From Cleveland to Paris & Beyond.
• Reward Yourself?
• .
• Medical Mcirobiology - A Complete High Yield Study Guide For Optometry Students (1)!

Welcome to Reddit, the front page of the internet. Become a Redditor and subscribe to one of thousands of communities. Want to add to the discussion? Specifically I want to know: Starting from a random processor, what is the average distance to another random processor?

1. Want to add to the discussion?.
2. Virus e batteri (Farsi unidea) (Italian Edition).
3. ASSASSIN!
4. What is Kobo Super Points?.

Manufacturing planning systems use simultaneous linear equations. Relational databases use set theory. For that I apologise.